投影对角化自旋激发
本文共 2031 字,大约阅读时间需要 6 分钟。
def Hamiltonian_H0_SU4(k,N,t=-1): """ t 是最近邻hopping系数 k 是Bloch波矢量 N 是宽度 """ A = np.matrix([[sqrt(3),0,1,np.exp(-1j*k)],[0, sqrt(3),1,1],[1,1,sqrt(3),0],[np.exp(1j*k),1,0,sqrt(3)]]) B = np.matrix([[0,0,0,0],[0,0,0,0],[1,0,0,0],[0,-1,0,0]]) H = tridiag(A,B,B.H,N) H[0,0] = 1000 return H
对角化得到本征值和本征向量
nk = 256N = 512k = np.linspace(0,2*pi,nk)band = np.zeros((4*N, nk))Ak = np.zeros((4*N,nk),dtype="complex")for i in range(nk): Hk0 = Hamiltonian_H0_SU4(k[i],N) E, A = LA.eigh(Hk0) band[:,i] = E Ak[:,i] = A[:,N-1]
画能带
for i in range(4*N): plt.plot(k,band[i,:])plt.ylim((-1,1))

测试本征态
plt.plot(Ak[:,1].real)
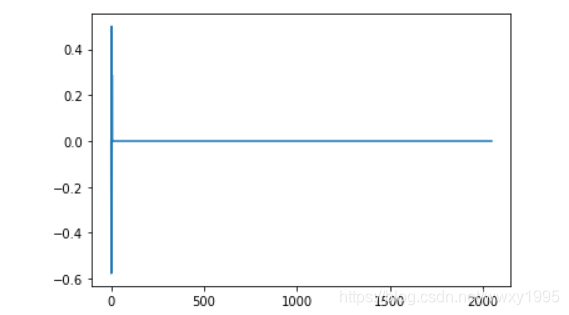
在基态基础上构造有效投影自旋激发哈密顿量
def Hamiltonian_Heff(nk,iq,Ak,U,N): H = np.zeros((nk,nk),dtype='complex') for j in range(nk): j_q = (j - iq + nk)%nk for i in range(j,nk): i_q = (i-iq + nk)%nk H[j,i] = -np.sum(Ak[:,i_q].conj()*Ak[:,i]*Ak[:,j_q]*Ak[:,j].conj()) H = H + H.T for i in range(nk): i_q = (i - iq + nk)%nk H[i,i] = np.sum(np.power(np.absolute(Ak),2).sum(axis=1)*np.power(np.absolute(Ak[:,i_q]),2)) return U*H/N
对角化并画能带图
for i in range(nk): plt.plot(k,band_mag[i,:])#plt.xlim((0,2*pi/3))plt.ylim((0,0.1))
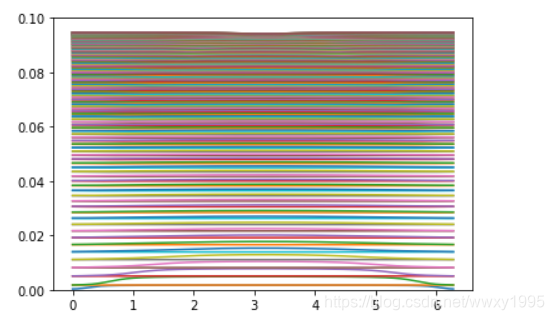
计算谱函数,用到一个矩阵循环移位技巧,实现函数如下:
def circshift(matrix,shiftnum1,shiftnum2): """ """ h,w=matrix.shape matrix=np.vstack((matrix[(h-shiftnum1):,:],matrix[:(h-shiftnum1),:])) matrix=np.hstack((matrix[:,(w-shiftnum2):],matrix[:,:(w-shiftnum2)])) return matrix
测试:
a=np.arange(1,17).reshape(4,4)print(a)b= circshift(a,0,2)print(b)
delta = 0.002nw = 256w = np.linspace(0,0.1,nw)Spectral_A = np.zeros((nw,nk),dtype='complex')for i in range(nk): A_kq = circshift(Ak,0,i) S_plus = np.sum(Ak.conj()*A_kq,axis=0).reshape(nk,1) for j in range(nw): for p in range(nk): Spectral_A[j,i] += np.absolute(np.dot(S_plus.conj().T,psi[:,p,i]))**2/(w[j]-band_mag[p,i]+1j*delta)
画谱函数
X,Y = np.meshgrid(k,w)plt.figure(figsize=(5,5))plt.pcolormesh(X, Y, -Spectral_A.imag/pi)plt.colorbar()
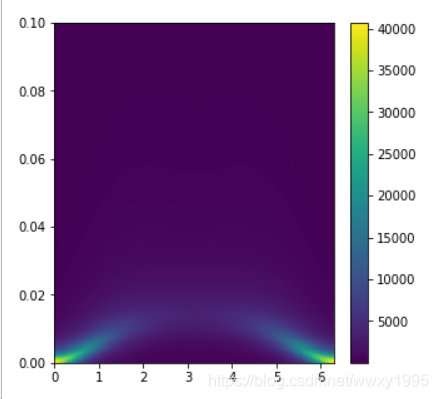
转载地址:http://wlqv.baihongyu.com/
你可能感兴趣的文章